카오스 법칙은 작은 초기 조건의 차이가 시간이 지남에 따라 예측 불가능하고 복잡한 결과를 가져오는 현상을 설명하는 개념입니다. 수학과 물리학을 포함한 여러 과학 분야에서 카오스 이론으로 불리며, 불확실하고 복잡한 시스템 내에서 어떻게 변화가 일어나는지를 탐구합니다.
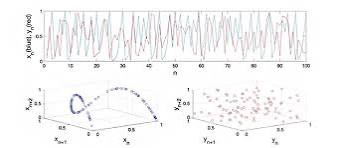
카오스 법칙의 주요 개념
1. 초기 조건의 민감성 (Sensitivity to Initial Conditions)
• 카오스 이론의 핵심은 “초기 조건에 대한 민감성”으로, 흔히 나비 효과로 설명됩니다. 나비가 베이징에서 날갯짓을 하면 그 작은 변화가 지구 반대편에서 태풍을 일으킬 수 있다는 비유에서 나온 개념입니다.
• 아주 미세한 초기 상태의 차이가 시간이 지남에 따라 시스템 전체에 큰 영향을 미칩니다. 예를 들어, 날씨 시스템은 초기 조건의 아주 작은 변화에도 큰 차이를 일으키며 예측이 어렵게 만듭니다.
2. 비선형성 (Nonlinearity)
• 카오스 시스템은 비선형적인 특징을 가지며, 이는 출력이 입력에 비례하지 않는다는 뜻입니다. 이 때문에 작은 변화가 예측 불가능하고 복잡한 결과로 이어집니다.
• 예를 들어, 인구 생태계나 경제 시스템에서 하나의 변화가 다른 요소들과 상호작용하면서 원래 예측한 것과는 다른 양상을 보일 수 있습니다.
3. 반복과 피드백 (Iteration and Feedback)
• 카오스 시스템은 반복과 피드백을 통해 복잡해지며, 특정 규칙이 계속해서 적용되면서 예측할 수 없는 패턴이 만들어집니다. 이런 반복 과정 속에서 시스템은 더욱 복잡한 형태로 발전합니다.
• 예를 들어, 물에 떠 있는 배가 매번 파도에 의해 다른 방향으로 이동하면서 점차적으로 예측 불가능한 궤적을 보이는 것이 반복과 피드백을 잘 보여줍니다.
4. 프랙탈 구조 (Fractal Structure)
• 카오스 이론은 프랙탈 구조와 관련이 있습니다. 프랙탈 구조란 같은 패턴이 반복되면서 자가 유사성을 보이는 구조로, 무작위적이지만 일정한 패턴을 보여줍니다.
• 예를 들어, 산의 모양, 구름의 형상, 해안선의 모습 등 자연계에 존재하는 여러 형태들이 프랙탈 패턴으로 설명됩니다.
카오스 법칙의 예
1. 날씨 예측
• 날씨는 초기 조건에 매우 민감한 대표적인 카오스 시스템입니다. 날씨의 작은 변화는 예측에 큰 영향을 미치므로, 멀리 떨어진 지역에서 발생하는 아주 작은 기후 변화도 날씨에 큰 영향을 줄 수 있습니다.
2. 금융 시장
• 금융 시장 역시 카오스 이론으로 설명됩니다. 주식 가격이나 환율 등은 초기 조건의 작은 변화로 인해 예측이 어렵고 비선형적인 특성을 띱니다.
3. 생태계와 인구 동태
• 생태계와 인구도 카오스 이론의 영향을 받습니다. 예를 들어, 포식자와 피식자의 관계에서 미세한 변화가 생태계 전체의 균형에 큰 영향을 미칠 수 있습니다.
요약
카오스 법칙은 단순한 시스템이라도 초기 조건에 따라 예측할 수 없는 복잡성과 변화를 보이는 것을 설명하는 이론입니다. 이로 인해 날씨, 금융, 생태계 등 다양한 영역에서의 불확실성과 복잡한 변동을 이해하는 데 중요한 개념으로 자리 잡았습니다.